What is a decision tree?
Decision Trees is a type of Supervised Machine Learning, where the data is continuously split according to a certain parameter. The leaves are the decisions or the final outcomes. They are iterative top-down construction methods for classifiers and also regression models.
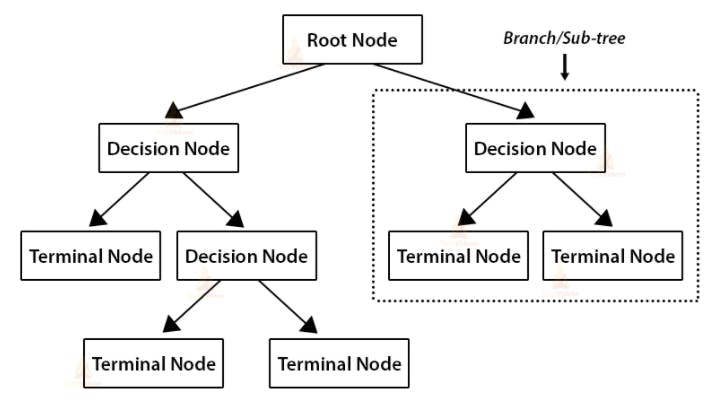
Root Node - First question/Decision we have.
Terminal Node/Leaf Node - Final Outputs.
Decision Node - The internal node that is not a root node.
Why are decision trees used in Machine Learning?
Decision Trees is used when the data points of the same class are located in different patches and we need to make perpendicular boundaries in order to classify them correctly.
Generic Tree Growing Algorithm:
- Pick the feature that, when the parent node is split, results in the largest information gain.
- Stop if Terminal/Child Nodes are pure or information gain <= 0.
- Go back to step 1 for each of the two child/terminal nodes.
Decision Tree Algorithms :
ID3 -- Iterative Dichotomizer 3
-Cannot handle numeric features.
-No pruning, prone to overfitting.
-Short and Wide trees.
-Maximizing Information gain.
-Binary and Multi-category features.
C4.5
-Supports both Continuous and Discrete features.
-Continuous is very expensive as it needs to consider all the possible ranges.
-Handles missing attributes (ignores them in gain compute).
-Post Pruning.
-Gain Ratio.
CART -- Classification and Regression Trees (Most Popular)
-Supports both Continuous and Discrete features.
-Strictly Binary trees, can generate better trees but tend to be larger and harder to interpret.
-Variance reduction in regression trees. (equal to Minimizing Mean Squared Error)
-Gini Impurity, tuning criteria in classification trees.
-Cost complexity pruning.
Terms:
Splitting Criteria - Criteria that can be used to decide which one is the good feature in order to perform splitting.
Variance Reduction - Reduction in Variance is a method for splitting the node used when the target variable is continuous, i.e., regression problems. It is so-called because it uses variance as a measure for deciding the feature on which node is split into child nodes. (Reduce Mean squared error)
Entropy - It is a measure of the randomness in the information being processed. The higher the entropy, the harder it is to draw any conclusions from that information. The best-case entropy is Zero.
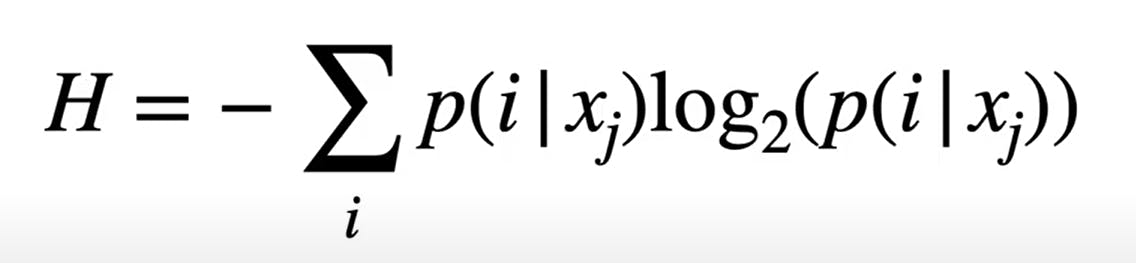
Information Gain - Information gain is a measure or an approach that allows us to access how good a given feature is. (Used for classification trees)
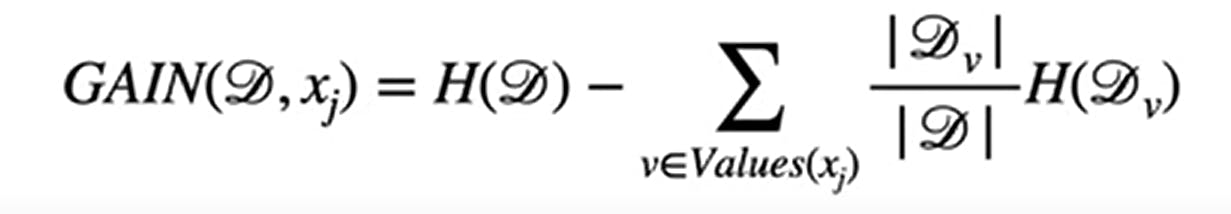This gives a scalar single number which we can compare to other features to find the best one. The goal is to maximize the information gain. The best The best-case information gain is equal to 1.
D - Dataset for the parent node.
Xj - Feature
H(D) (Impurity) - Entropy of parent node but now we also use the Gini impurity function.
H(Dv) - Entropy for a subset of the data. (Multi category split)
Gini Impurity - Gini Impurity is a measurement of the likelihood of incorrect classification of a new instance of a random variable.
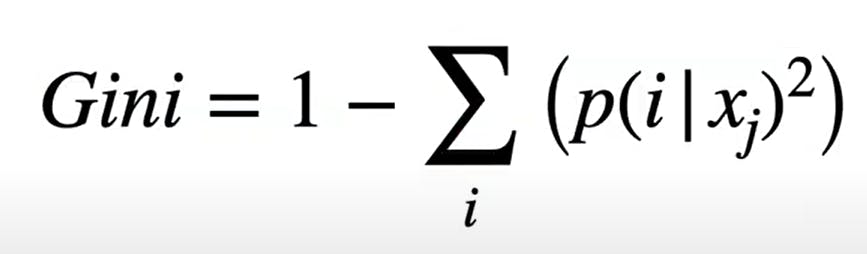i --> Class label
Gini & Entropy Vs Misclassification Error :
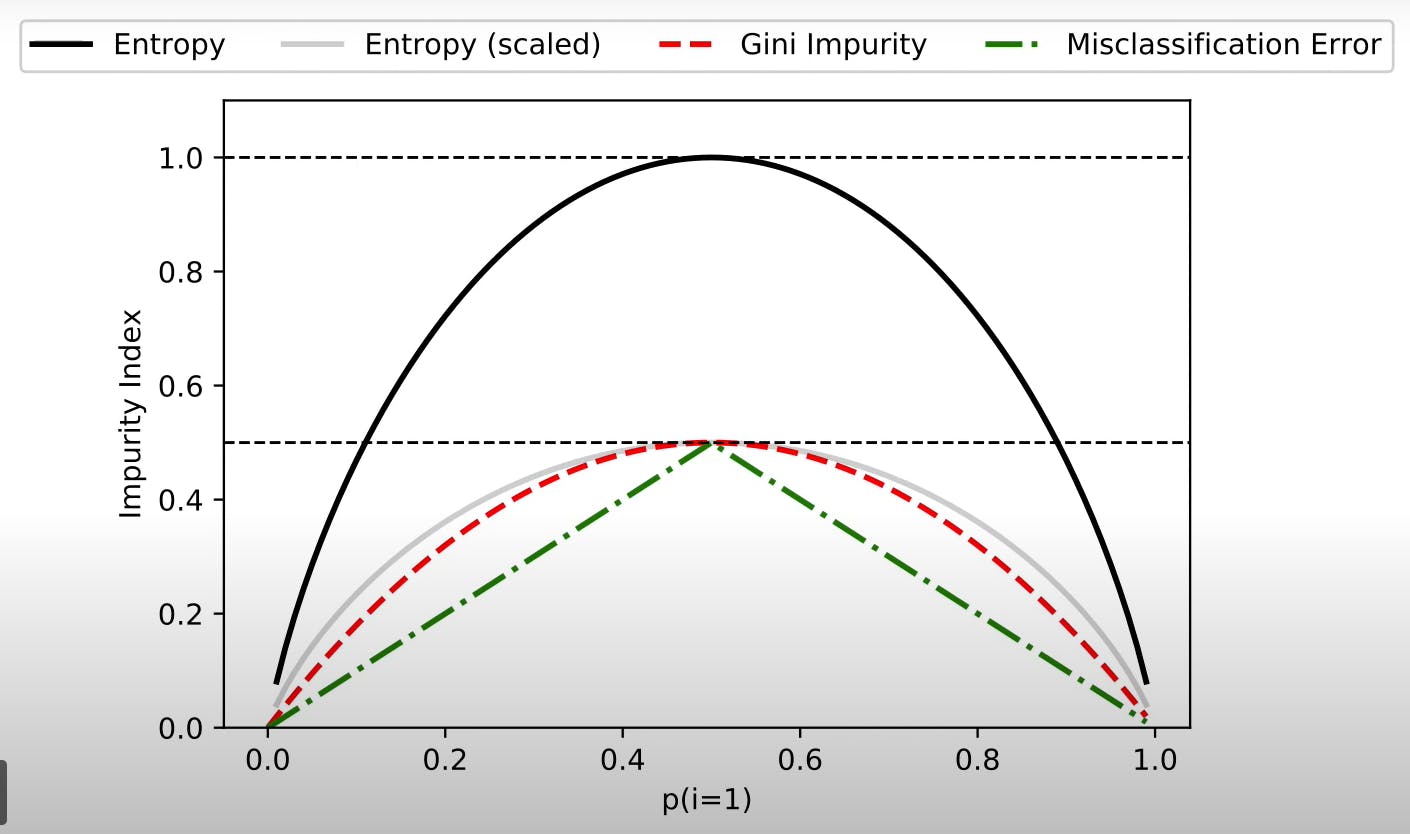The entropy is concave whereas the misclassification error is straight. This has an impact on why entropy is better than misclassification. We can sometimes get stuck if the information gain is zero because the misclassification error is not concave and has a straight line.
Improvements and dealing with Overfitting :
- Gain Ratio - Modification of the information gain that reduces the bias. It helps to avoid overfitting. If a feature has more categories, for example, unique values for each row (eg. Row ID) which is equal to the training set size then it is a bad feature. The value of the gain ratio should be high.
Shortcomings -
Cannot separate the two categories with the help of a diagonally straight line as it can only split on one feature at a time (Staircase type decision boundary), which would be a super deep decision tree and an expensive model and prone to overfitting.
Decision trees fit the training set well, so it has very good performance on the training set. However for new data, even from the same distribution, it won't fit well because of the deeper decision trees.
Solution:
Pre-Pruning
- Set a Maximum tree depth
- Stop growing if split is not statistically significant
- Set a minimum number of data points for each node.
- We set the total number of nodes as a tuning parameter.
Post-Pruning
- Grow the full tree first, then remove nodes in C4.5.
- Reduced error pruning, remove nodes via the validation set evaluation.
- Can convert trees to rules first, then prune the rules.
Pros and Cons of decision trees :
- (+) Easy to interpret and communicate.
- (+) Can represent complete hypothesis space.
- (-) Easy to overfit.
- (-) Elaborate pruning required.
- (-) Expensive to just fit a diagonal line.
- (-) Output range is bounded in regression trees.
Hope you found it helpful 😊